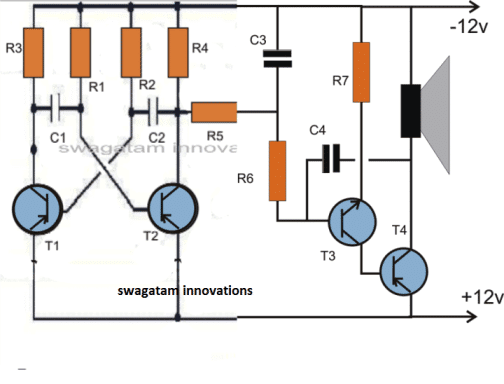
Matematika hrá rozhodujúcu úlohu pri porozumení správania a práce elektrický a elektronických systémov . Polynómy, algebra, pravdepodobnosť, integrácie a diferenciácie atď. Tvoria významnú súčasť nástrojov používaných na riešenie systémov. S rastúcou zložitosťou systémov sú potrebné veľmi sofistikované metódy. Diferenciálne rovnice sa prominentne používajú na definovanie riadiacich systémov. Tieto rovnice sa dajú ľahko vyriešiť. Ale zložitosť vzniká pri riešení diferenciálnych rovníc vyššieho rádu. Na riešenie takýchto zložitých diferenciálnych rovníc vyššieho rádu sa osvedčila matematická metóda Laplaceova transformácia . Pretože sa táto transformácia často využíva, je užitočné vedieť, na čo skutočne slúžili a ako fungujú.
Čo je to Laplaceova transformácia?
V matematike sa transformácie používajú na transformáciu premennej z jednej formy na druhú, aby sa s rovnicou ľahko manipulovalo. Laplace transformuje do veľkej miery to isté. Transformujú diferenciálnu rovnicu vyššieho rádu do polynomiálnej formy, ktorá je oveľa ľahšia ako priame riešenie diferenciálnej rovnice.
Existujú ale rôzne transformácie ako Fourierova transformácia, z transformuje to, čo robí Laplaceovu transformáciu špeciálnou? Hlavnou výhodou Laplaceovej transformácie je, že sú definované pre stabilné aj nestabilné systémy, zatiaľ čo Fourierove transformácie sú definované iba pre stabilné systémy.
Vzorec Laplaceovej transformácie
Laplaceova transformácia funkcie f (t) v časovej oblasti, kde t je skutočné číslo väčšie alebo rovné nule, sa uvádza ako F (s), kde existuje  s je komplexné číslo vo frekvenčnej doméne. tj. s = σ + jω
s je komplexné číslo vo frekvenčnej doméne. tj. s = σ + jω
Vyššie uvedená rovnica sa považuje za jednostranný Laplaceova transformačná rovnica . Keď sa limity rozšíria na celú skutočnú os, potom Bilaterálna Laplaceova transformácia možno definovať ako
 V praktických obvodoch ako Obvody RC a RL zvyčajne sa používajú počiatočné podmienky, takže na účely analýzy sa použijú jednostranné Laplaceove transformácie.
V praktických obvodoch ako Obvody RC a RL zvyčajne sa používajú počiatočné podmienky, takže na účely analýzy sa použijú jednostranné Laplaceove transformácie.
Pretože s = σ + jω, keď σ = 0 Laplaceova transformácia sa správa ako Fourierova transformácia.

Laplaceove transformačné vzorce
Podmienky použiteľnosti Laplaceovej transformácie
Laplaceove transformácie sa nazývajú integrálne transformácie, takže sú potrebné podmienky pre konvergenciu týchto transformácií.
 tj f musí byť lokálne integrovateľný pre interval [0, ∞) a v závislosti od toho, či je σ kladné alebo záporné, e ^ (- σt) môže klesať alebo rásť. Pre bilaterálne Laplaceove transformácie namiesto jednej hodnoty integrál konverguje v určitom rozmedzí hodnôt známych ako oblasť konvergencie.
tj f musí byť lokálne integrovateľný pre interval [0, ∞) a v závislosti od toho, či je σ kladné alebo záporné, e ^ (- σt) môže klesať alebo rásť. Pre bilaterálne Laplaceove transformácie namiesto jednej hodnoty integrál konverguje v určitom rozmedzí hodnôt známych ako oblasť konvergencie.
Vlastnosti Laplaceovej transformácie:
Lineárnosť

Lineárnosť
Časový posun

Časový posun
Posun v S-doméne

Posun v S-doméne
Obrátenie času

Obrátenie času
Diferenciácia v S-doméne

Diferenciácia v S-doméne
Konvolúcia v čase

Konvolúcia v čase
Veta o počiatočnej hodnote
Veta o počiatočnej hodnote sa použije, keď je pri Laplaceovej transformácii stupeň čitateľa menší ako stupeň menovateľa  Veta o konečnej hodnote:
Veta o konečnej hodnote:
Ak všetky póly sF (s) ležia v ľavej polovici S-roviny, použije sa veta o konečnej hodnote.
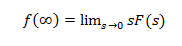 Inverzná Laplaceova transformácia
Inverzná Laplaceova transformácia
Vďaka konvergenčnej charakteristike majú Laplaceova transformácia aj inverznú transformáciu. Laplaceove transformácie vykazujú mapovanie jedna k jednej z jedného funkčného priestoru do druhého. Vzorec pre inverznú Laplaceovu transformáciu je
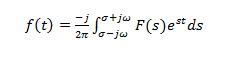 Ako vypočítať Laplaceovu transformáciu?
Ako vypočítať Laplaceovu transformáciu?
Laplaceova transformácia uľahčuje manipuláciu s rovnicami. Keď je daná diferenciálna rovnica vyššieho rádu, použije sa na ňu Laplaceova transformácia, ktorá prevedie rovnicu na algebraickú rovnicu, čím sa uľahčí jej manipulácia. Potom vypočítame korene zjednodušením tejto algebraickej rovnice. Teraz sa nachádza inverzná Laplaceova transformácia jednoduchšieho výrazu, ktorá rieši danú diferenciálnu rovnicu vyššieho rádu.

Výpočet Laplaceovej transformácie
Aplikácie Laplaceovej transformácie
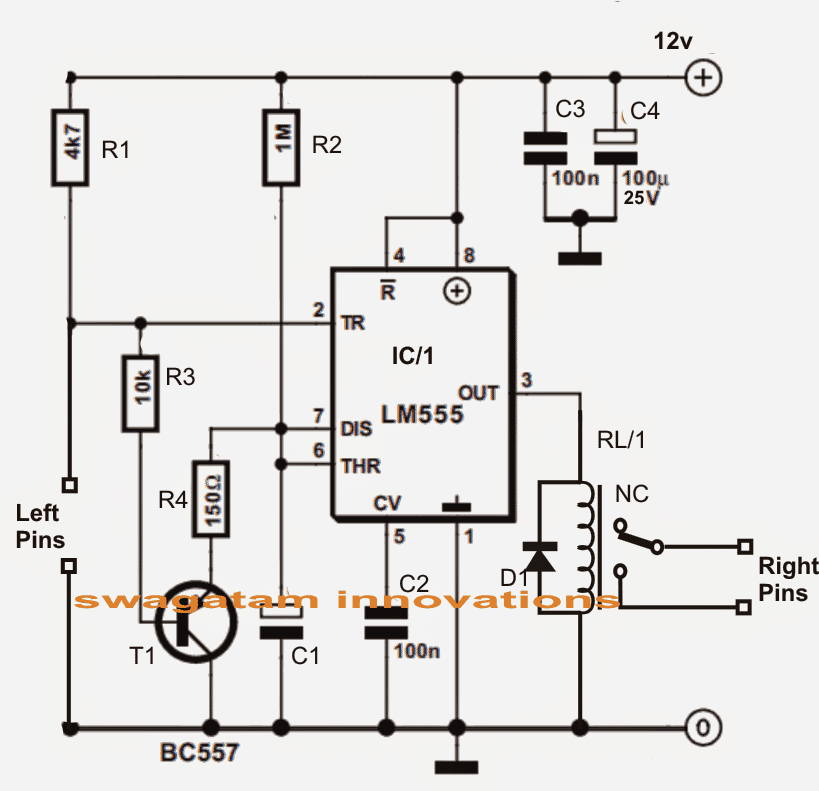
- Analýza elektrických a elektronické obvody .
- Rozkladanie zložitých diferenciálnych rovníc na jednoduchšie polynomické formy.
- Laplaceova transformácia poskytuje informácie o ustálených aj prechodných stavoch.
- V strojovom učení sa Laplaceova transformácia používa na vytváranie predpovedí a vykonávanie analýz pri dolovaní údajov.
- Laplaceova transformácia zjednodušuje výpočty v modelovaní systému.
Aplikácia Laplaceovej transformácie pri spracovaní signálu
Laplaceove transformácie sa často rozhodujú pre spracovanie signálu. Spolu s Fourierovou transformáciou Laplaceova transformácia sa používa na štúdium signálov vo frekvenčnej doméne. Keď sú v signáli vo frekvenčnej doméne malé frekvencie, potom sa dá očakávať, že signál bude v časovej doméne hladký. Filtrovanie signálu sa zvyčajne vykonáva vo frekvenčnej doméne, pre ktorú Laplace slúži ako dôležitý nástroj na konverziu signálu z časovej domény na frekvenčnú doménu.
Aplikácia Laplaceovej transformácie v riadiacich systémoch
Kontrolné systémy sú zvyčajne určené na riadenie správania iných zariadení. Príklad riadiace systémy môže siahať od jednoduchého domáceho vykurovacieho regulátora až po priemyselný riadiaci systém, ktorý reguluje chovanie strojov.
Všeobecne platí, že riadiaci inžinieri používajú diferenciálne rovnice na opis správania rôznych funkčných blokov uzavretej slučky. Na riešenie týchto rovníc sa tu používa Laplaceova transformácia bez straty rozhodujúcich informácií o premenných.
Charakterizácia lineárnych časovo premenných systémov pomocou Laplaceovej transformácie
Pre príležitostný systém ROC spojený so systémom je funkciou pravá polovičná rovina. Systém je anti-ležérny, ak jeho impulzná odpoveď h (t) = 0 pre t> 0.
Ak ROC systémových funkcií H (s) obsahuje os jω, potom L.T.I. systém sa nazýva stabilný systém. Ak má príležitostný systém s racionálnymi funkciami systému H (s) záporné reálne časti pre všetky jeho póly, potom je systém stabilný.
Laplaceova transformácia je teda rozhodujúcim nástrojom pri analýze obvodov. Môžeme povedať, že stetoskop je pre lekára, Laplaceove transformácie sú pre riadiaceho inžiniera. Čo považujete za Laplaceove transformácie? V čom vám boli nápomocné?
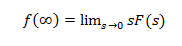 Inverzná Laplaceova transformácia
Inverzná Laplaceova transformácia 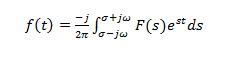 Ako vypočítať Laplaceovu transformáciu?
Ako vypočítať Laplaceovu transformáciu?