Charakteristiky prenosu

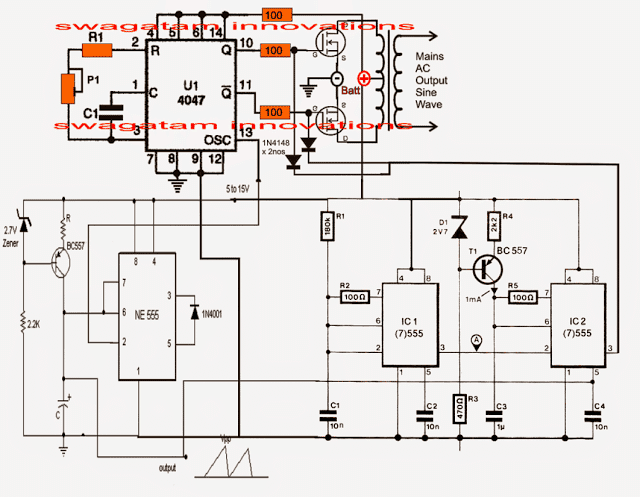
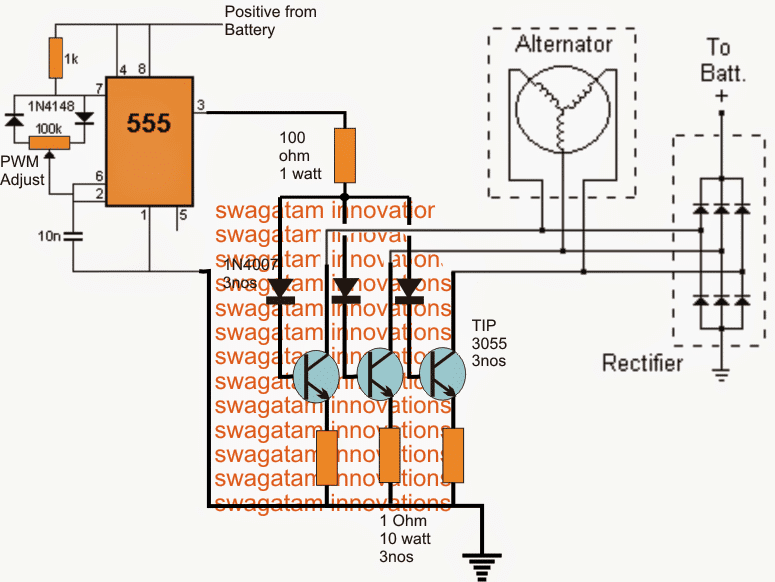
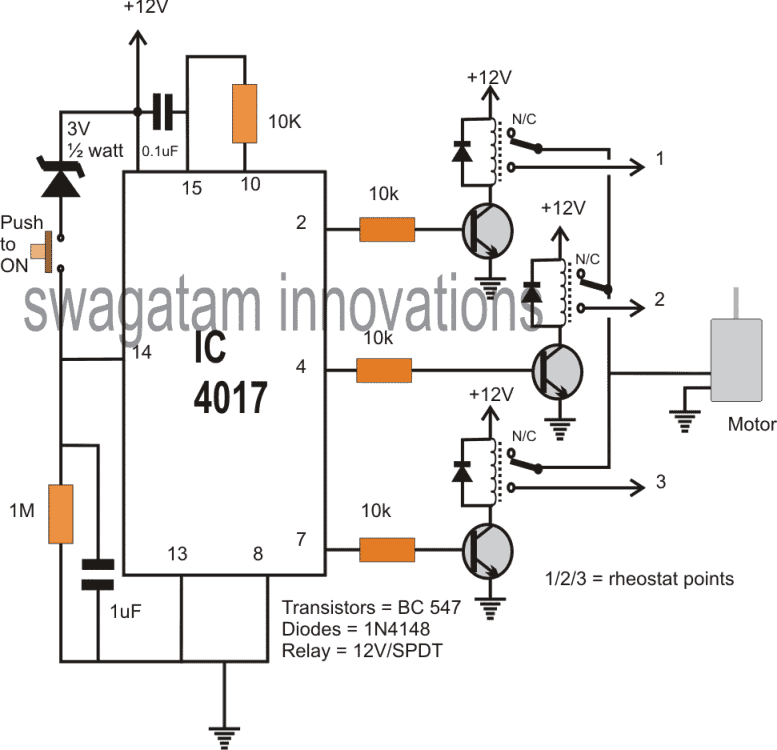
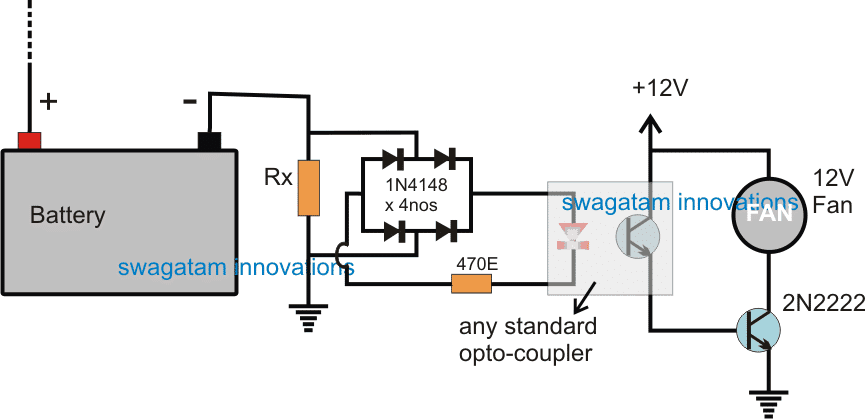
V tranzistoroch je možné prenosové charakteristiky chápať ako vykreslenie výstupného prúdu proti vstupnej veličine, ktorá následne vykazuje priamy „prenos“ premenných zo vstupu na výstup v krivke znázornenej v grafe.

Vieme, že pre bipolárny prechodový tranzistor (BJT) sú výstupný kolektorový prúd IC a riadiaci vstupný bázový prúd IB spojené parametrom beta , ktorá sa pre analýzu považuje za konštantnú.

S odkazom na nižšie uvedenú rovnicu nájdeme lineárny vzťah existujúci medzi IC a IB. Ak urobíme úroveň IB 2x, potom sa tiež IC proporčne zdvojnásobí.

Je však smutné, že tento pohodlný lineárny vzťah nemusí byť v JFET dosiahnuteľný naprieč ich vstupnými a výstupnými veľkosťami. Vzťah medzi ID odtokového prúdu a hradlovým napätím VGS je skôr definovaný vzťahom Shockleyho rovnica :

Tu sa stáva štvorcový výraz zodpovedný za nelineárnu odozvu naprieč ID a VGS, čo vedie k exponenciálne rastúcej krivke, keď sa veľkosť VGS zmenšuje.

Aj keď by bolo jednoduchšie implementovať matematický prístup pre dc analýzu, grafický spôsob môže vyžadovať vykreslenie vyššie uvedenej rovnice.

To môže prezentovať príslušné zariadenie a vykreslenie sieťových rovníc týkajúcich sa rovnakých premenných.

Riešenie nájdeme pohľadom na priesečník dvoch kriviek.

Pamätajte, že keď použijete grafickú metódu, vlastnosti zariadenia zostanú neovplyvnené sieťou, v ktorej je zariadenie implementované.

Keď sa zmení priesečník medzi týmito dvoma krivkami, zmení sa tým aj sieťová rovnica, čo však nemá žiadny vplyv na prenosovú krivku definovanú vyššie uvedeným ekvivalentom, 5.3.

Všeobecne teda môžeme povedať, že:

Prenosová charakteristika definovaná Shockleyovou rovnicou nie je ovplyvnená sieťou, v ktorej je zariadenie implementované.

Prenosovú krivku môžeme získať pomocou Shockleyovej rovnice alebo z výstupných charakteristík ako je znázornené na obr. 5.10

Na obrázku nižšie vidíme dva grafy. Zvislá čiara meria pre obidva grafy miliampéry.

Jeden graf vykresľuje ID odtokového prúdu verzus napätie VDS od zdroja k zdroju, druhý graf vykresľuje odtokový prúd verzus napätie brány od zdroja alebo ID vs VGS.

Pomocou charakteristík odtoku zobrazených na pravej strane osi „y“ dokážeme nakresliť vodorovnú čiaru začínajúcu v oblasti nasýtenia krivky znázornenej ako VGS = 0 V až k osi zobrazenej ako ID.

Aktuálna úroveň takto dosiahnutá pre dva grafy je IDSS.

Priesečník na krivke ID vs VGS bude uvedený nižšie, pretože vertikálna os je definovaná ako VGS = 0 V

Všimnite si, že charakteristiky odtoku ukazujú vzťah medzi jednou veľkosťou výstupu odtoku s ďalšou veľkosťou výstupu odtoku, pričom dve osi sú interpretované premennými v rovnakej oblasti charakteristík MOSFET.

Prenosové charakteristiky možno teda definovať ako graf vybíjacieho prúdu MOSFET verzus množstvo alebo signál pôsobiaci ako vstupná regulácia.

To následne vedie k priamemu „prenosu“ cez vstupné / výstupné premenné, keď sa použije krivka vľavo na obrázku 5.15. Keby to bol lineárny vzťah, bol by graf ID vs VGS priamou čiarou cez IDSS a VP.

To však má za následok parabolickú krivku spôsobenú vertikálnym rozstupom medzi VGS presahujúcimi charakteristiky odtoku, ktorá sa na obrázku 5.15 významne zmenšuje, pretože VGS je čoraz negatívnejší.

Ak porovnáme priestor medzi VGS = 0 V a VGS = -1V s priestorom medzi VS = -3 V a pinch-off, vidíme, že rozdiel je identický, aj keď pre hodnotu ID je veľmi odlišný.

Sme schopní identifikovať ďalší bod na prenosovej krivke nakreslením vodorovnej čiary od VGS = -1 V krivky až po os ID a následným predĺžením k druhej osi.

Všimnite si, že VGS = - 1 V na spodnej osi prenosovej krivky, keď ID = 4,5 mA.

Upozorňujeme tiež, že v definícii ID pri VGS = 0 V a -1 V sa používajú úrovne nasýtenia ID, zatiaľ čo ohmická oblasť je zanedbávaná.

Pohybom ďalej vpred, s VGS = -2 V a - 3V, sme schopní dokončiť graf prenosovej krivky.

Ako použiť Shockleyovu rovnicu

Prenosovú krivku na obrázku 5.15 môžete tiež priamo dosiahnuť použitím Shockleyovej rovnice (rovnica 5.3) za predpokladu, že sú uvedené hodnoty IDSS a Vp.

Úrovne IDSS a VP definujú limity krivky pre dve osi a vyžadujú iba vykreslenie niekoľkých medziľahlých bodov.

Pravosť Shockleyho rovnica Rovnicu 5.3 ako zdroj prenosovej krivky na obr. 5.15 možno dokonale vyjadriť kontrolou určitých rozlišovacích úrovní konkrétnej premennej a následným identifikovaním zodpovedajúcej úrovne druhej premennej, a to nasledujúcim spôsobom:

Toto sa zhoduje s grafom znázorneným na obr. 5.15.

Sledujte, ako opatrne sa pri vyššie uvedených výpočtoch riadia záporné znamienka pre VGS a VP. Vynechanie čo i len jedného záporného znamienka by mohlo viesť k úplne nesprávnemu výsledku.

Z vyššie uvedenej diskusie je celkom zrejmé, že ak máme hodnoty IDSS a VP (ktoré sa dajú odkázať z údajového listu), môžeme rýchlo určiť hodnotu ID pre akúkoľvek veľkosť VGS.

Na druhej strane, prostredníctvom štandardnej algebry môžeme odvodiť rovnicu (pomocou rovnice 5.3) pre výslednú úroveň VGS pre danú úroveň ID.

Dá sa to odvodiť celkom jednoducho, ak chceme získať:

Teraz si overme vyššie uvedenú rovnicu určením úrovne VGS, ktorá produkuje odtokový prúd 4,5 mA pre MOSFET, ktorý má charakteristiky zodpovedajúce obr. 5.15.

Výsledok overuje rovnicu, pretože je v súlade s obr. 5.15.

Použitie skratkovej metódy

Pretože potrebujeme vykresľovať krivku prenosu pomerne často, mohlo by sa nám hodiť získať skratkovú techniku ​​na vykreslenie krivky. Žiaducou metódou by bolo umožniť používateľovi vykresliť krivku rýchlo a efektívne bez toho, aby bola dotknutá presnosť.

Rovnica 5.3, ktorú sme sa naučili vyššie, je navrhnutá tak, aby konkrétne úrovne VGS produkovali úrovne ID, ktoré je možné pamätať na použitie ako body vykreslenia pri kreslení prenosovej krivky. Ak zadáme VGS ako 1/2 odštiepovacej hodnoty VP, výslednú hladinu ID môžeme určiť pomocou Shockleyovej rovnice nasledujúcim spôsobom:

Je potrebné poznamenať, že vyššie uvedená rovnica nie je vytvorená pre konkrétnu úroveň VP. Rovnica je všeobecná forma pre všetky úrovne VP, pokiaľ je VGS = VP / 2. Výsledok rovnice naznačuje, že odtokový prúd bude vždy 1/4 úrovne nasýtenia IDSS, pokiaľ napätie medzi vstupným a výstupným zdrojom má hodnotu, ktorá je o 50% nižšia ako hodnota odštiepenia.

Upozorňujeme, že úroveň ID pre VGS = VP / 2 = -4V / 2 = -2V podľa obr. 5.15

Opting ID = IDSS / 2 a jeho dosadenie do Rovnice 5.6 dostaneme nasledujúce výsledky:

Aj keď je možné stanoviť ďalšie počet bodov, dostatočnej úrovne presnosti je možné jednoducho dosiahnuť nakreslením prenosovej krivky iba pomocou 4 bodov vykreslenia, ako je uvedené vyššie a tiež v tabuľke 5.1 nižšie.

Vo väčšine prípadov môžeme použiť iba bod vykreslenia pomocou VGS = VP / 2, zatiaľ čo osové priesečníky pri IDSS a VP nám poskytnú krivku dostatočne spoľahlivú pre väčšinu analýz.