Základné sieťové teorémy používané v sieťovej analýze sú dostupné v rôznych typoch, ako je Thévenin, superpozícia, Norton, substitúcia, maximálny prenos energie, reciprocita a Millmanove vety . Každá veta má svoje vlastné aplikačné oblasti. Takže pochopenie každej sieťovej vety je veľmi dôležité, pretože tieto vety možno použiť opakovane v rôznych obvodoch. Tieto vety nám pomáhajú pri riešení zložitých sieťových obvodov pre danú podmienku. Tento článok pojednáva o jednom z typov sieťovej vety substitučná veta – príklady.
Čo je substitučná veta?
Výrok substitučnej vety je; že vždy, keď je známy prúd v celej vetve alebo napätie v ktorejkoľvek vetve v sieti, potom môže byť vetva zmenená kombináciou rôznych prvkov, ktoré vytvoria podobné napätie a prúd v tejto vetve. Inými slovami, môže byť definovaný ako; pre ekvivalenciu vetvy by tepelné napätie aj prúd mali byť rovnaké.
Koncept substitučnej vety závisí hlavne od substitúcie jedného prvku iným prvkom. Táto veta je tiež veľmi užitočná pri dokazovaní niektorých ďalších teorémov. Hoci táto veta nie je použiteľná na riešenie vety, ktorá zahŕňa vyššie uvedené dva zdroje, ktoré nie sú zapojené ani sériovo, ani paralelne.
Vysvetlenie substitučnej vety
Kroky, ktoré sú súčasťou riešenia substitučnej vety, zahŕňajú najmä nasledujúce.
Krok 1: Najprv musíme nájsť napätie a prúd všetkých prvkov siete. Vo všeobecnosti možno napätie a prúd vypočítať pomocou ohmového zákona, Kirchoffove zákony ako KVL alebo KCL.
Krok 2: Vyberte požadovanú vetvu, ktorú chcete odstrániť, prostredníctvom iného prvku, ako je zdroj napätia/odpor a zdroj prúdu.
Krok 3: Nájdite správnu hodnotu nahradeného prvku za predpokladu, že napätie a prúd by sa nemali meniť.
Krok 4: Skontrolujte nový obvod jednoduchým výpočtom prúdu a napätia všetkých prvkov a vyhodnoťte ho pôvodnou sieťou.
Schéma obvodu substitučnej vety
Pomocou nasledujúcej schémy zapojenia ľahko pochopíme substitučnú vetu. Vieme, že substitučná veta je náhradou jedného prvku iným ekvivalentným prvkom. Ak je akýkoľvek prvok v rámci siete nahradený/nahradený zdrojom prúdu alebo zdrojom napätia, ktorého prúd a napätie v rámci prvku alebo naprieč prvkom zostanú nezmenené ako v predchádzajúcej sieti.
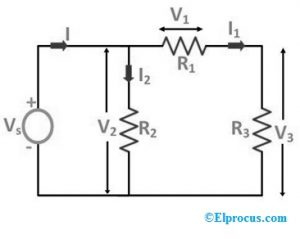
Rôzne odpory ako R1, R2 a R3 sú pripojené jednoducho cez zdroj napätia. Tok prúdu „I“ pretekajúci obvodom je rozdelený na I1 a I2, kde „I1“ je privádzaný cez odpor „R1“ a „I2“ prúdi cez odpor R2, ako je znázornené v obvode. Tu sú poklesy napätia na odporoch R1, R2 a R3 zodpovedajúcim spôsobom V1, V2 a V3.
Ak je teraz odpor „R3“ nahradený zdrojom napätia „V3“, ako je znázornené na nasledujúcej schéme zapojenia nižšie:
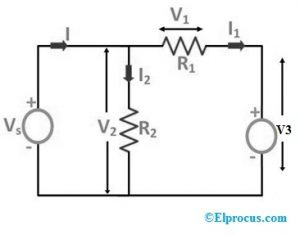
V nasledujúcej schéme zapojenia je odpor „R3“ nahradený tokom prúdu cez tento prvok „I1“.
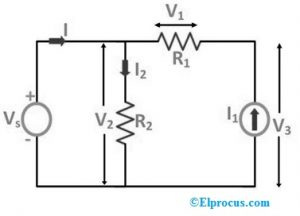
Z vyššie uvedených dvoch prípadov, ak je prvok nahradený zdrojom prúdu alebo napätia, počiatočné podmienky obvodu sa nemenia, to znamená, že napájanie napätím na odpore a napájanie prúdu v celom odpore sa nezmení, aj keď sú nahradené iným zdrojov.
Príklady problémov
Príklady substitučnej vety sú diskutované nižšie.
Príklad1:
Vyriešte nasledujúci obvod pomocou substitučnej vety na výpočet napätia a prúdu vo všetkých odporoch.
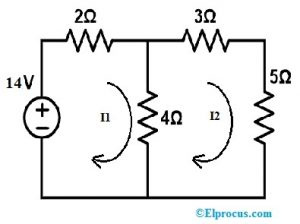
Krok 1:
Najprv aplikujte KVL na slučku1 vo vyššie uvedenom obvode
14 = 6I1 – 4I2 ….(1)
Aplikujte KVL na slučku 2 vo vyššie uvedenom obvode
0 = 12I2 – 4I1
12 I2 = 4I1 => I1 = 3I2……….(2)
Dosaďte túto rovnicu 2 do vyššie uvedenej rovnice 1.
14 = 6(3I2) - 4I2
14 = 18I2 – 4I2 => 14I2 => 1A
I2 = 1A
Z vyššie uvedenej rovnice (2)
I1 = 3I2
Vieme, že I2 = 1A
I1 = 3A
Krok 2:
V tomto kroku musíme odstrániť vetvy loop1, aby sme vytvorili jednu slučku.
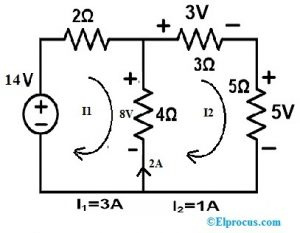
Krok 3:
Na miesto rezistora 4Ω môžeme umiestniť zdroj prúdu/zdroj napätia. Teraz použijeme zdroj prúdu.
Tok prúdu cez slučku 2 v obvode je 1A. Takže nahradíme vetvu zdrojom prúdu 1A. V dôsledku toho je zvyškový obvod uvedený nižšie.
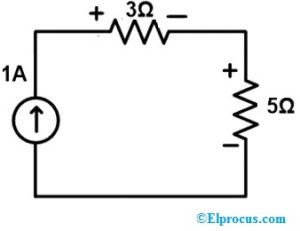
Krok 4:
V tomto kroku je potrebné skontrolovať napätie a prúd všetkých prvkov. Vyššie uvedený obvod obsahuje jednu slučku, t.j. zdroj prúdu. Hodnota pretekajúceho prúdu v slučke je teda podobná hodnote zdroja prúdu.
Tu je aktuálna hodnota zdroja 1A. Takže tok prúdu cez odporové vetvy 3Ω a 5Ω je 1A, čo je podobné pôvodnej sieti.
Pomocou ohmov zákon nájdite hodnotu napätia na rezistore 3Ω
V = IS
V = I x R
V = 1 x 3 => 3 V.
Podobne pomocou zákona ohmov musíme nájsť hodnotu napätia na rezistore 5Ω.
V = IS
V = I x 5
V = 1 x 5 => 5 V.
Prúd a napätie sú teda podobné pôvodnej sieti. Takže takto funguje táto veta.
Ak teraz v kroku 3 zvolíme zdroj napätia namiesto zdroja prúdu. Takže v tomto stave je hodnota zdroja napätia podobná hodnote vetvy 4Ω odporu.
Tok prúdu cez 4Ω odporovú vetvu v rámci pôvodnej siete je
I1 – I2 => 3 – 1 => 2A
Podľa Ohmovho zákona;
Napätie na rezistore 4Ω je V = 2 x 4 = 8V
Potrebujeme teda pripojiť zdroj napätia s 8V do siete a zvyškový obvod je znázornený na obrázku nižšie.
V = 2 x 4 = 8 V
Potrebujeme teda pripojiť 8V zdroj napätia k sieti a zvyšný obvod je taký, ako je znázornené na obrázku nižšie.
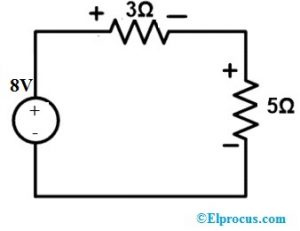
Použite KVL na vyššie uvedenú slučku na overenie napätia a prúdu.
8 = 3I + 5I => 8I
I = 1A.
Použitím ohmového zákona možno vypočítať napätie na rezistore 3Ω ako;
V = 1 × 3 => 3 V
Podobne je napätie na rezistore 5Ω;
V = 1 × 5 => 5 V
Napätie a prúd sú teda po výmene rovnaké ako v pôvodnej sieti.
Príklad2:
Zoberme si nasledujúci obvod na aplikáciu substitučnej vety.
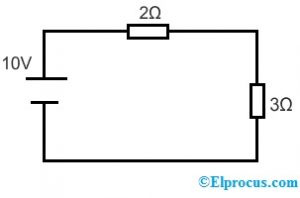
Podľa pravítka delenia napätia je napätie na rezistoroch 2Ω a 3Ω;
Napätie na rezistore 3Ω je
V = 10×3/3+2 = 6V
Napätie na rezistore 2Ω je
V = 10×2/3+2 = 4V
Prietok prúdu v obvode sa vypočíta ako I = 10/3+2 = 2A.
Ak vo vyššie uvedenom obvode nahradíme 6V zdroj napätia namiesto odporu 3Ω, obvod bude vyzerať takto.
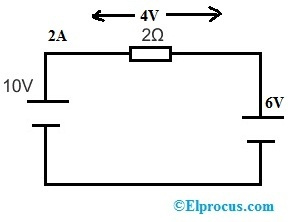
Na základe Ohmovho zákona je napätie na odpore 2Ω a tok prúdu v obvode
V = 10-6 => 4 V
I = 10-6/2 = 2A
Ak namiesto odporu 3Ω nahradíme zdroj prúdu 2A, obvod bude vyzerať takto.
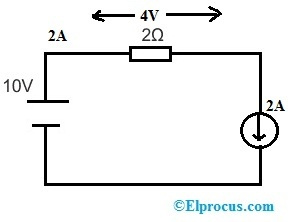
Napätie na rezistore 2Ω je V = 10 – 3* 2 => 4 V & napätie na zdroji prúdu „2A“ je V = 10 – 4 => 6 V. Takže napätie na rezistore 2Ω a prúd v obvode sa nezmenia.
Výhody
The výhody substitučnej vety zahŕňajú nasledujúce.
- Tento koncept vety závisí hlavne od substitúcie jedného prvku iným prvkom.
- Táto veta poskytuje intuíciu o správaní obvodu a tiež pomáha pri overovaní rôznych iných sieťových teorémov.
- Výhodou použitia tejto vety je, že táto veta poskytuje správne hodnoty pre premenné ako X & Y, ktoré zodpovedajú priesečníku.
Obmedzenia
The obmedzenia substitučnej vety zahŕňajú nasledujúce.
- Túto vetu nemožno použiť na riešenie siete, ktorá obsahuje minimálne dva alebo viac zdrojov, ktoré nie sú v rámci série/paralel.
- V tejto vete by sa pri výmene prvku nemalo meniť správanie obvodu.
Aplikácie
The aplikácie substitučnej vety zahŕňajú nasledujúce.
- Substitučná veta sa používa na dokázanie mnohých ďalších teorémov.
- Táto veta je užitočná pri riešení sústavy rovníc v matematike.
- Táto veta nahrádza jeden prvok obvodu jedným ďalším prvkom.
- Táto veta sa používa na analýzu obvodov so závislými zdrojmi.
Na ktorom okruhu neplatí substitučná veta?
Obvod, ktorý má vyššie uvedené dva zdroje, ktoré sú zapojené buď paralelne alebo sériovo, potom táto substitučná veta nie je použiteľná.
Prečo sa kompenzačná veta nazýva substitúcia?
Obidve vety ako kompenzácia a substitúcia sú rovnaké z hľadiska postupu a redukcie. Takže táto veta je použiteľná pre antény a nazýva sa aj substitučná veta.
Ako používate substitučnú vetu?
Túto vetu možno použiť nahradením ktorejkoľvek vetvy inou vetvou v rámci siete bez toho, aby došlo k narušeniu napätí a prúdov v celej sieti. Takže táto veta sa používa v lineárnych aj nelineárnych obvodoch.
Čo je substitučná vlastnosť?
Substitučná vlastnosť uvádza, že ak je premenná „a“ ekvivalentná inej premennej „b“, potom „a“ možno nahradiť namiesto „b“ v akomkoľvek výraze alebo rovnici & „b“ možno nahradiť namiesto „ a' v akomkoľvek výraze alebo rovnici.
Ide teda o všetko prehľad suplovania veta – obvod s príkladmi. Tu je otázka pre vás, čo je to kompenzačná veta?