Vety o elektrických obvodoch sú vždy užitočné pri hľadaní napätia a prúdov v obvodoch s viacerými slučkami. Tieto vety používajú na analýzu základné pravidlá alebo vzorce a základné matematické rovnice základné komponenty elektrickej alebo elektroniky parametre, ako sú napätia, prúdy, odpor atď. Medzi tieto základné vety patria základné vety ako Superpositionova veta, Tellegenova veta, Nortonova veta, veta o maximálnom prenose energie a Theveninova veta. Ďalšia skupina sieťových viet, ktoré sa väčšinou používajú v procese analýzy obvodu, zahŕňajú vetu o kompenzácii, vetu o substitúcii, vetu o reciprocite, Millmanovu vetu a Millerovu vetu.
Vety o sieti
Všetky sieťové vety sú stručne popísané nižšie.
1. Veta o superpolohe
Veta o superpozícii je spôsob, ako určiť prúdy a napätia prítomné v obvode, ktorý má viac zdrojov (berúc do úvahy jeden zdroj súčasne). Veta o superpozícii tvrdí, že v lineárnej sieti, ktorá má množstvo zdrojov alebo odporov napätia alebo prúdu, je prúd cez ktorúkoľvek vetvu siete algebraický súčet prúdov, ktoré vznikajú pri pôsobení každého zo zdrojov, keď konajú nezávisle.

Veta o super pozícii
Veta o superpozícii sa používa iba v lineárnych sieťach. Táto veta sa používa v obvodoch striedavého aj jednosmerného prúdu, kde pomáha budovať ekvivalentné obvody Thevenin a Norton.
Na vyššie uvedenom obrázku je obvod s dvoma zdrojmi napätia rozdelený na dva jednotlivé obvody podľa tvrdenia tejto vety. Jednotlivé obvody tu uľahčujú vzhľad celého obvodu. A opätovnou kombináciou týchto dvoch obvodov po individuálnom zjednodušení je možné ľahko nájsť parametre, ako je pokles napätia pri každom odpore, napätie uzla, prúdy atď.
2. Theveninova veta
Vyhlásenie: Lineárna sieť pozostávajúca z množstva zdrojov napätia a odporov môže byť nahradená ekvivalentnou sieťou, ktorá má jeden zdroj napätia nazývaný Theveninovo napätie (Vthv) a jediný odpor nazývaný (Rthv).

Theveninova veta
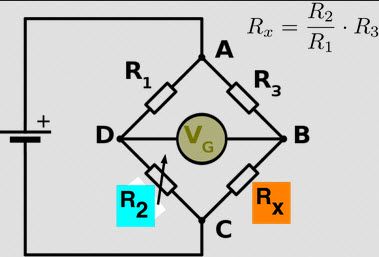
Vyššie uvedený obrázok vysvetľuje, ako je táto veta použiteľná pre analýzu obvodu. Thevinensovo napätie sa počíta podľa daného vzorca medzi svorkami A a B prerušením slučky na svorkách A a B. Rovnako sa Thevinensov odpor alebo ekvivalentný odpor počíta zo zdroja skratového napätia a zdrojov otvoreného obehového prúdu, ako je to znázornené na obrázku.
Túto vetu je možné aplikovať na lineárne aj bilaterálne siete. Používa sa hlavne na meranie odporu pomocou Wheatstoneovho mostíka.
3. Nortonova veta
Táto veta uvádza, že akýkoľvek lineárny obvod obsahujúci niekoľko zdrojov energie a odporov môže byť nahradený jediným generátorom konštantného prúdu paralelne s jediným rezistorom.

Nortonova veta
Je to rovnaké ako v prípade Thevinensovej vety, v ktorej nájdeme ekvivalentné hodnoty napätia a odporu podľa Thevinensa, tu sú však určené súčasné ekvivalentné hodnoty. Proces hľadania týchto hodnôt je uvedený v príklade na vyššie uvedenom obrázku.
4. Veta o maximálnom prenose energie
Táto veta vysvetľuje podmienky pre maximálny prenos energie do záťaže za rôznych obvodových podmienok. Veta hovorí, že prenos energie zdrojom na záťaž je v sieti maximálny, keď sa odpor záťaže rovná vnútornému odporu zdroja. Pre striedavé obvody by sa impedancia záťaže mala zhodovať s impedanciou zdroja pre maximálny prenos energie, aj keď záťaž pracuje odlišne výkonové faktory .

Veta o maximálnom prenose energie
Napríklad vyššie uvedený obrázok zobrazuje schému zapojenia, kde je obvod zjednodušený až na úroveň zdroja s vnútorným odporom pomocou Theveninovej vety. Prenos sily bude maximálny, keď sa tento odpor Thevinens bude rovnať odporu záťaže. Praktická aplikácia tejto vety zahŕňa audio systém, v ktorom musí byť odpor reproduktora prispôsobený zosilňovač audio výkonu na získanie maximálneho výkonu.
5. Veta o reciprocite
Veta o reciprocite pomáha nájsť ďalšie zodpovedajúce riešenie aj bez ďalšej práce, hneď ako sa obvod analyzuje na jedno riešenie. Veta hovorí, že v lineárnej pasívnej bilaterálnej sieti možno zdroj excitácie a jej zodpovedajúcu odozvu zameniť.

Veta o reciprocite
Na vyššie uvedenom obrázku je prúd vo vetve R3 I3 s jedným zdrojom vs. Ak je tento zdroj nahradený vetvou R3 a dôjde k skratu zdroja na pôvodnom mieste, potom je prúd prúdiaci z pôvodného miesta I1 rovnaký ako prúd I3. Takto môžeme nájsť zodpovedajúce riešenia pre obvod, akonáhle je obvod analyzovaný s jedným riešením.
6. Veta o kompenzácii

Veta o kompenzácii
Ak sa v ktorejkoľvek bilaterálnej aktívnej sieti zmení veľkosť impedancie z pôvodnej hodnoty na inú hodnotu prenášajúcu prúd I, potom sú výsledné zmeny, ktoré sa vyskytujú v iných vetvách, rovnaké ako zmeny, ktoré by boli spôsobené zdrojom vstrekovacieho napätia. v modifikovanej vetve so záporným znamienkom, tj mínus napäťového prúdu a zmenený súčin impedancie. Štyri vyššie uvedené obrázky ukazujú, ako je táto kompenzačná veta použiteľná pri analýze obvodov.
7. Millmanova veta

Millmanova veta
Táto veta uvádza, že ak paralelne pracuje ľubovoľný počet zdrojov napätia s konečným vnútorným odporom, je možné ich nahradiť jedným zdrojom napätia so sériovo ekvivalentnou impedanciou. Ekvivalentné napätie pre tieto paralelné zdroje s vnútornými zdrojmi v Millmanova veta sa počíta z nižšie uvedeného vzorca, ktorý je uvedený na obrázku vyššie.
8. Tellegenova veta

Tellegenova veta
Táto veta je použiteľná pre obvody s lineárnymi alebo nelineárnymi, pasívnymi alebo aktívnymi a hysterickými alebo nehysterickými sieťami. Uvádza sa v ňom, že súčet okamžitého výkonu v obvode s n počtom vetví je nulový.
9. Veta o substitúcii
Táto veta uvádza, že ktorúkoľvek vetvu v sieti je možné nahradiť inou vetvou bez narušenia prúdov a napätí v celej sieti za predpokladu, že nová vetva má rovnakú sadu koncových napätí a prúdu ako pôvodná vetva. Substitučnú vetu je možné použiť v lineárnych aj nelineárnych obvodoch.
10. Millerova veta

Millerova veta
Táto veta uvádza, že v lineárnom obvode, ak existuje vetva s impedanciou Z spojenou medzi dvoma uzlami s uzlovými napätiami, je možné túto vetvu nahradiť dvoma vetvami spájajúcimi príslušné uzly so zemou dvoma impedanciami. Aplikácia tejto vety nie je len efektívnym nástrojom na vytvorenie ekvivalentného obvodu, ale aj nástrojom na navrhovanie ďalších modifikovaných prvkov elektronické obvody impedanciou.
Toto sú všetky základné vety o sieti, ktoré sa široko používajú v analýze elektrických alebo elektronických obvodov. Dúfame, že ste mohli mať nejaké základné predstavy o všetkých týchto vetách.
Pozornosť a záujem, s ktorým ste si prečítali tento článok, sú pre nás skutočne povzbudivé, a preto očakávame vaše ďalšie záujmy týkajúce sa akýchkoľvek iných tém, projektov a diel. Takže nám môžete napísať o svojich pripomienkach, komentároch a návrhoch v sekcii komentárov uvedenej nižšie.
Fotoúvery
- Veta o super pozícii podľa keywon
- Theveninova veta podľa hyperfyzika
- Nortonova veta podľa hyperfyzika
- Veta o maximálnom výkone energie podľa allaboutcircuits
- Veta o reciprocite podľa netlecturer
- Tellegenova a kompenzačná veta od electronicspani
- Millmanova veta podľa myelektrický
- Millerova veta podľa